图形学 线性代数基础
本篇内容均取自https://www.bilibili.com/video/BV1X7411F744
本篇为 1 - 3 集笔记
向量的点积
-
如何求出单位向量 => 向量 / 向量的长度 = 单位向量
-
在不给出说明的情况下,向量的默认的表示形式其实是竖着的
$$ \vec{A} = \begin{pmatrix} x \ y \end{pmatrix} A^T = (x,y) $$$$ T是上标 转置了 $$ -
向量的长度 = sqr(x² + y²)
-
向量点乘得到的是一个数
$$ \vec{a} · \vec{b} = \vec{||a||} ·\vec{||b||}· cos0 $$ -
取得两个向量的夹角 a 的单位向量 × b的
$$ \cos \theta = \frac{\vec{a} \cdot \vec{b}}{||\vec{a}|| \, ||\vec{b}||} $$
$$ ||\vec{a}|| = 向量的长度$$
$$ ||\vec{a}|| = \sqrt{x^2 + y^2} $$
- 向量的点成就是两个数相乘然后加起来
闲话
向量b对于向量a的垂直 是 向量b(popu 垂直)
向量b(popu)的方向是向量a对应的方向
向量b(popu) = k * 向量a的单位向量
向量b(popu)的长度 = b的长度 * a与b的夹角余弦
k= ||向量b(popu)|| = ||向量b|| cos0
向量a和b的点积就是夹角余弦
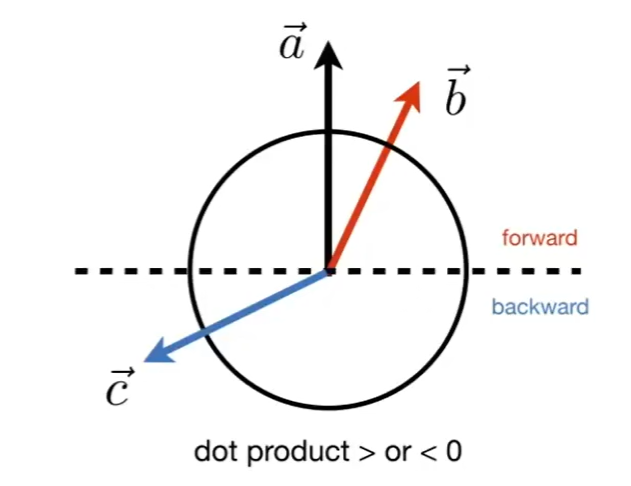
- 如果向量同向 那么两个向量点乘会得到大于0的值
如果向量不同向 那么两个向量的点乘会得到小于0的值
点乘也会可以告诉我们两个向量有多接近,越接近1就越近,1 - 0 是垂直 0 - -1相反
向量的叉积
-
$$
\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})
$$$$
|| \mathbf{a} \times \mathbf{b} || = || \mathbf{a} || \cdot || \mathbf{b} || \cdot \sin(\theta)
$$
叉乘不满足交换律,
a x b 结果与 b x a相反,新向量与 a b 垂直如果
x 叉乘 y 得到 z那就说他是右手坐标系一个向量叉乘自己 = 0
长度为0的向量 -
用于判断左和右,上和下
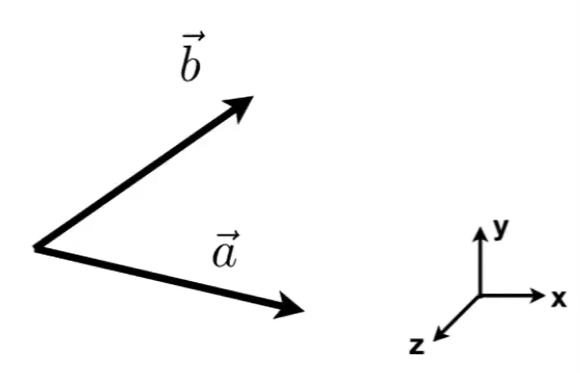
向量
a叉乘b得到的结果z轴是正的,那么说明b在a的左侧
-
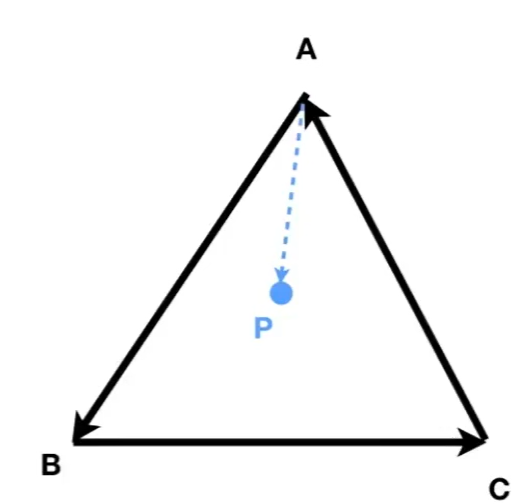
判断某点是否在三角形内部(光栅化基础)
AB叉乘AP得到左侧BC叉乘BP得到 P点在BC的左侧CA叉乘CP得到 P点在CA的左侧如果是顺时针 那么就在右侧,得到0自己决定
-
标准正坐标系
$$ || \mathbf{u} || = || \mathbf{v} || = || \mathbf{w} || = 1 $$$$ \mathbf{u} \cdot \mathbf{v} = \mathbf{v} \cdot \mathbf{w} = \mathbf{u} \cdot \mathbf{w} = 0 $$
矩阵
-
乘以一个数就是将矩阵内的每个数都乘以这个数
-
(M x N)(N x P) = (M x P)只有 N N相等才有意义第一个矩阵的列数必须等于第二个矩阵的行数
如下面,上面的矩阵乘以下面的矩阵 等于第三个矩阵
比如结果的第二行四列,我们找到第一个矩阵的第二行,第二个矩阵的第四列 然后乘起来相加
(5,2) * (4,3) = (20,6) = 26
|
|
-
矩阵的乘积不满足任何交换率,但满足结合律和分配律
$$ (\mathbf{AB})\mathbf{C} = \mathbf{A}(\mathbf{BC}) $$$$ \mathbf{A}(\mathbf{B} + \mathbf{C}) = \mathbf{AB} + \mathbf{AC} $$$$ (\mathbf{A} + \mathbf{B})\mathbf{C} = \mathbf{AC} + \mathbf{BC} $$ -
矩阵与向量相乘,向量是竖着的
列向量m×1,这样就有意义了,左边的矩阵只要是 (n,m)就能乘 -
转置
$$ \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{pmatrix} -> \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{pmatrix} $$$$ 乘积的转置\\ (\mathbf{AB})^T = \mathbf{B}^T \mathbf{A}^T $$(ij -> ji)对角线为分割线,然后两边值位置互换,对角线下去只有两列,最终结果就是两行 -
单位矩阵 他是一个对角阵
$$ 单位矩阵\\ \mathbf{I}_{3\times3} \begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{pmatrix} $$$$ AA^{-1} = A^{-1} = I\\\\ 矩阵的逆:\\ (AB)^{-1}=B^{-1} A^{-1} $$ -
点乘向量的矩阵形式
$$ \begin{pmatrix} x_a & y_a & z_a \end{pmatrix} \begin{pmatrix} x_b\\ y_b\\ z_b \end{pmatrix}= (x_{a}x_{b} + y_{a}y_{b} + z_{a}z_{b} ) $$ -
向量的叉积矩阵形式
$$ 叉积矩阵形式 A^{*}是矩阵\\ a \times b = A^{*}b = \begin{pmatrix} 0 && -z_{a} && y_{a}\\ z_{a} &&0 && -x_{a}\\ -y_{a} && x_{a} && 0 \end{pmatrix} \begin{pmatrix} x_{b}\\ y_{b}\\ z_{b} \end{pmatrix} $$
图形学 变换
-
缩放矩阵
$$ 左矩阵\\ \begin{pmatrix} s & 0\\ 0 & s \end{pmatrix} $$$$ \begin{pmatrix} x'\\ y' \end{pmatrix}= \begin{pmatrix} s & 0\\ 0 & s \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix} $$图像大小缩放s倍 xy的s单独设置可以单独缩放 -
反转
$$ \begin{pmatrix} x'\\ y' \end{pmatrix} => \begin{pmatrix} -x\\ y \end{pmatrix} $$$$ \begin{pmatrix} -1 & 0\\ 0 & 1 \end{pmatrix} \times \begin{pmatrix} x\\ y \end{pmatrix} $$(x,y) => (-x,y) -
切变
$$ \begin{pmatrix}x'\\y'\end{pmatrix}=\begin{pmatrix}1 & a\\0 & 1\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix} $$ -
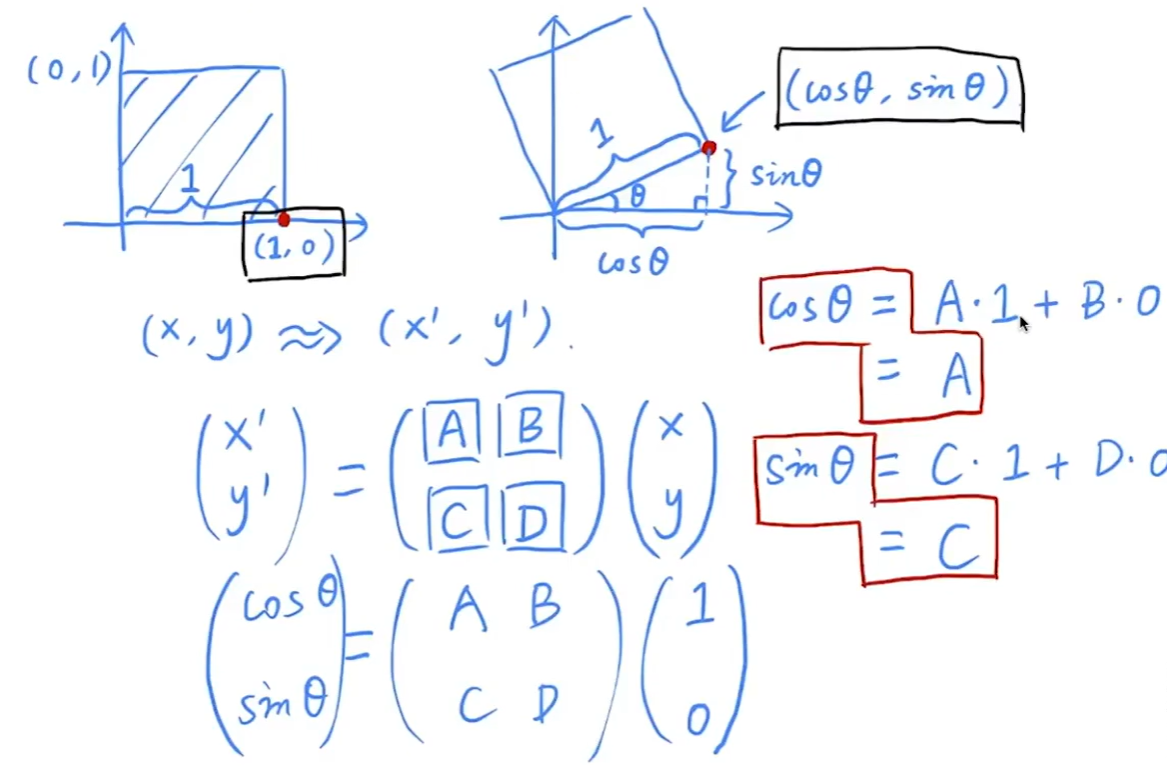
旋转(2维)

-
共性
x'=Mx要使用相同维度的矩阵乘以向量
$$ x' = a_x + b_y\\ y' = c_x + d_y $$$$ \begin{pmatrix} a & b\\ c & d \end{pmatrix} ✖ \begin{pmatrix} x\\ y \end{pmatrix} $$
其次坐标
平移变换
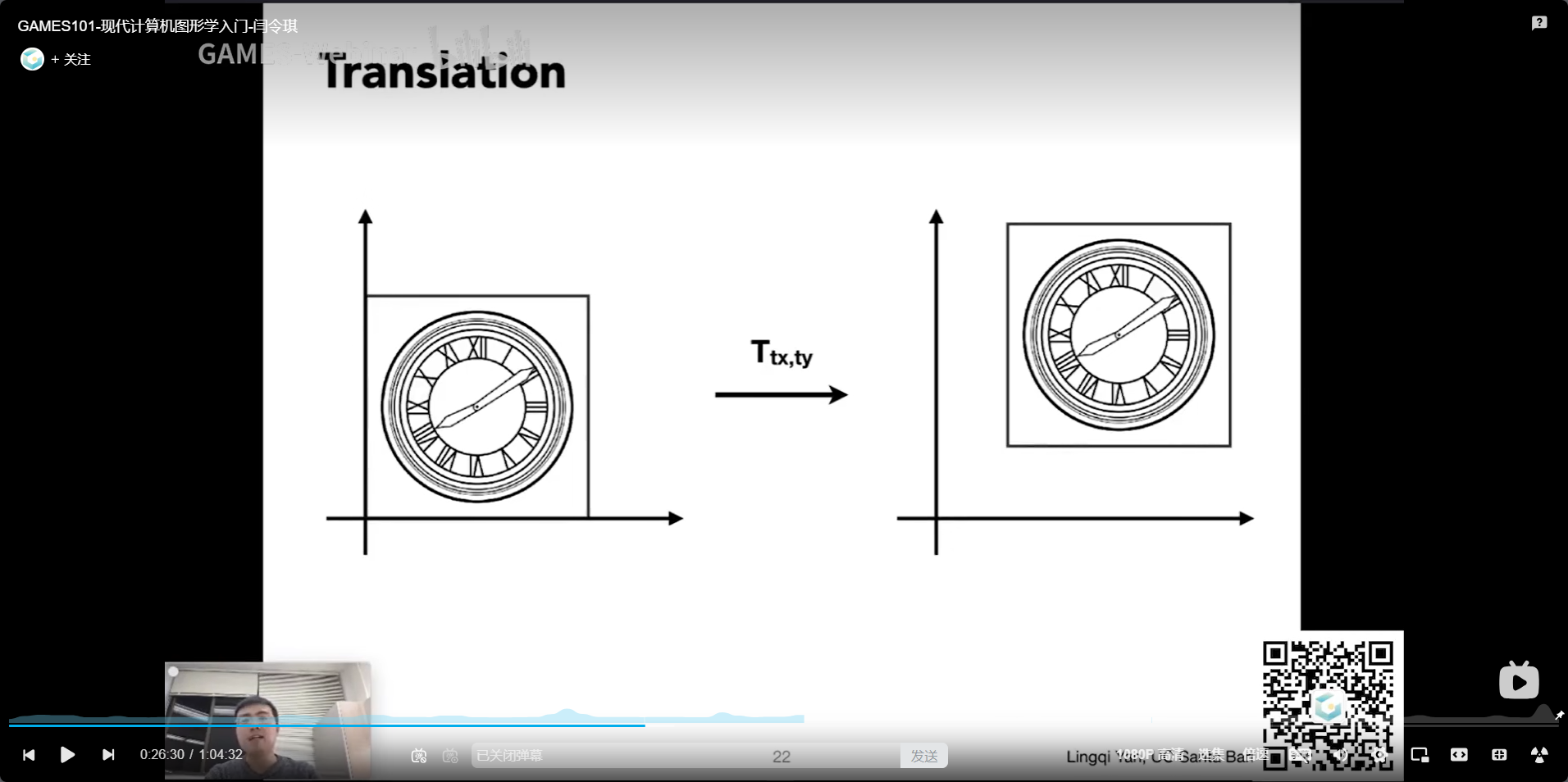 $$
x'=x+t_x\\
x'=y+t_y
$$
$$
x'=x+t_x\\
x'=y+t_y
$$$$ {平移的矩阵表示} abcd是单位矩阵10,01\\ \begin{pmatrix} x'\\ y' \end{pmatrix}= \begin{pmatrix} a & b\\ c & d \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix} + \begin{pmatrix} t_x\\ t_y \end{pmatrix} $$平移使用矩阵的形式表示,不属于线性变换
线性变换必须表示为 一个向量等于一个矩阵乘以另一个向量
$$ 2D Point = (x,y,1)^T\\ 2D Vector= (x,y,0)^T $$为了不将平移排除在基础变换之外,“懒”的科学家们发明了新的东西,引入了新的形式来表示物体的坐标,为二维的坐标增加一个维度
如果是表示一个点,那么为1,如果为了表示一个向量那么值为0
$$ xy1是二维的一个点\\ \begin{pmatrix} x'\\ y'\\ w' \end{pmatrix}= \begin{pmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{pmatrix}· \begin{pmatrix} x\\ y\\ 1 \end{pmatrix}= \begin{pmatrix} x + t_x\\ y + t_y\\ 1 \end{pmatrix} $$增加了一个维度后会发现有了更好的性质
引入其次坐标最大的目的就是为了通过增加一个维度的方式,将平移变换也写成矩阵x向量的形式
- 向量表示方向性,向量具有平移不变性,为了保护向量,所以将向量的z设置为0,保证他不变
$$ \begin{pmatrix} x\\ y\\ w \end{pmatrix}is~the~2D~point~ \begin{pmatrix} x/w\\ y/w\\ 1 \end{pmatrix}, w ≠ 0 $$在齐次坐标中,任何的 x / y / w 作为一个二维的点,表示的点是
x除以w,y除以w, 1
$$ point + point = ?? $$在w不等于0的情况下,可以把xyw都除以w,第三个维度就1了,表示的就是一个点了
xyw表示的一个点就是
x/w, y/w(二维的点)在上面的公式中
$$ point + point = 这两个点的中点\\ \begin{pmatrix} ((x_1+x_2)/w)\\ ((y_1+y_2)/w)\\ w/w \end{pmatrix} $$如果把z变为1呢 ,这边的w是2,因为上面算过了
仿射变换
$$ \begin{pmatrix} x'\\ y'\\ \end{pmatrix} = \begin{pmatrix} a & b\\ c & d\\ \end{pmatrix}· \begin{pmatrix} x\\ y\\ \end{pmatrix} + \begin{pmatrix} t_x\\ t_y\\ \end{pmatrix} $$仿射变换就行线性变换和平移变换的组合
$$ 仿射变换的齐次坐标形式\\ \begin{pmatrix} x'\\ y'\\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x\\ c & d & t_y\\ 0 & 0 & 1 \end{pmatrix}· \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} $$如果使用其次坐标表示2维的仿射变换
- 最后一行永远是
0,0,1- 平移永远写在最后一列的头两位数
- abcd是原来线性变换的一部分
线性变换的其次坐标形式
$$ S(s_x,s_y) = \begin{pmatrix} s_x & 0 & 0\\ 0 & s_y & 0\\ 0 & 0 & 1 \end{pmatrix} $$缩放
$$ R(\alpha) = \begin{pmatrix} cos~\alpha & -sin~\alpha & 0\\ sin~\alpha & cos~\alpha & 0\\ 0 & 0 & 1 \end{pmatrix} $$旋转
$$ T(t_x,t_y)= \begin{pmatrix} 1 & 0 & t_x\\ 0 & 1 & t_y\\ 0 & 0 & 1 \end{pmatrix} $$平移
因为没有进行线性变换 所以是 10 01
变换的分解
连续变换的应用是从右往左的
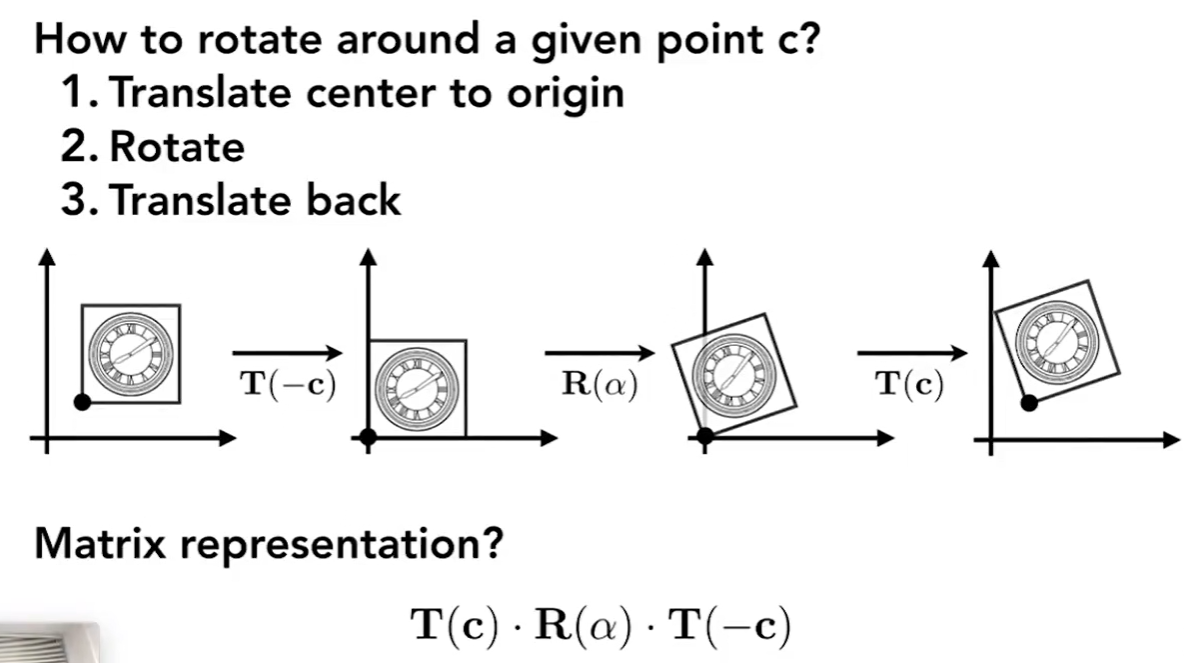
逆变换
逆变换就是将变换的操作反过来
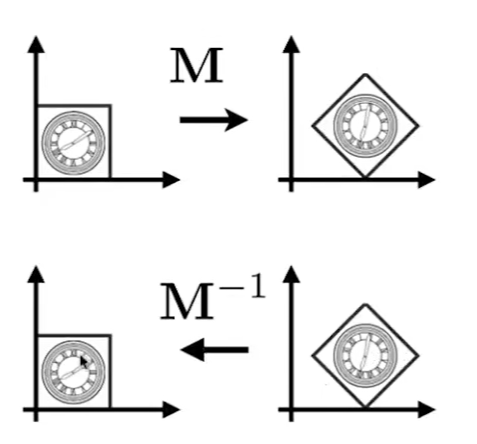
一个矩阵乘以他自己的逆矩阵一定等于单位矩阵 做了一遍操作,再做一遍反的操作,就相当于什么都没做
3维变换
$$ \begin{pmatrix} x'\\ y'\\ z'\\ 1 \end{pmatrix} = \begin{pmatrix} a & b & c & t_x\\ d & e & f & t_y\\ g & h & i & t_z\\ 0 & 0 & 0 & 1 \end{pmatrix}· \begin{pmatrix} x\\ y\\ z\\ 1 \end{pmatrix} $$与二维基本一致,先应用线性变换再平移
